В 4:27 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.
Вопрос вызвавший трудности
Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике "ЕГЭ (школьный)". Ваш вопрос звучал следующим образом: ‘Точка S не лежит в плоскости параллелограмма ABCD. Докажите, что линия пересечения плоскостей SAB и SCD параллельна плоскости параллелограмма.’
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
решение задания по геометрии
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
Самсонова Агата Аркадьевна — автор студенческих работ, заработанная сумма за прошлый месяц 86 400 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.
В треугольной пирамиде SABC все ребра равны друг другу. На ребре SA взята точка M такая, что SM = MA, на ребре SB — точка N такая, что SN : SB = 1 : 3. Через точки M и N проведена плоскость, параллельная медиане AD основания ABC. Найти отношение объема треугольной пирамиды, отсекаемой от исходной проведенной плоскостью, к объему пирамиды SABC.
Для построения искомого сечения проведем дополнительно апофему SD в боковой грани SBC, а затем отложим отрезок ME в треугольнике SAD параллельно стороне AD: так как ME || AD и M — середина AS, то E — середина SD. Тогда получаем, что MNE — искомая плоскость. Осталось показать, что продолжение NE падает в точку B, то есть точка E лежит на отрезке NB.
Для этого можно отдельно рассмотреть треугольник SBC и провести в нем дополнительный отрезок DL параллельно стороне NE. По теореме Фалеса из угла CSD получаем
Так как BD = DC, а NL = NC, то получаем, что DL является средней линией для треугольника BNC, то есть
Таким образом получили, что MNB — искомое сечение тетраэдра, и оно отсекает от него треугольную пирамиду BMNS. Заметим, что если рассмотреть в качестве основания полученной пирамиды треугольник SMN, то высота, проведенная из точки B на плоскость SMN, совпадает с высотой пирамиды SABC. Из формулы для объема пирамиды получаем (считаем для удобства, что все ребра равны 1):
№ 37(устно). SABCD – правильная пирамида. Как построить линию пересечения плоскостей граней SAD и SBC, SAB и SDC? Ответ обосновать.
№ 38(устно). Изобразить параллелограмм ABCD и точку Р, не лежащую в плоскости этого параллелограмма. Отметить точки E, K, M, H – середины сторон AB, BC, CD и AD соответственно. Как построить линию пересечения плоскостей PEH и PKM? Ответ обосновать.
№ 39(устно).АВСDA1B1C1D1 — куб. Как построить линию пересечения плоскости DA1C1 и плоскости грани АВС? Ответ обосновать.
№ 40 . Основание пирамиды SABCD – трапеция ABCD. Построить сечение пирамиды плоскостью, проходящей через ребро AD и точку М, принадлежащую грани BSC.
План построения.
4. AKND – сечение.
5. Доказать, что сечение искомое.
№ 41. Треугольники ABC и DBC не лежат в одной плоскости и имеют общую сторону, точки М, Н и К – середины соответственно сторон BD, CD, AC. 1) Построить l линию пересечения плоскостей МКН и АВС. 2) Построить точку Р пересечения плоскости МКН и прямой АВ. 3) Найти РК, если ВС=8.
4) Доказать, что отрезки РН и МК пересекаются и в точке пересечения делятся пополам.
1. 2. 3.4.
1) План построения. 3)
1. Прямая l: lÌ ABC, KÎl, l || BC. 1. PK– средняя линия DBAC.
2. Доказать, что l – искомая линия 2. PK=4.
пересечения плоскостей. 4)
2) План построения. 1.KH – параллелограмм,
1. P= l Ç AB. MK, PH – диагонали.
2. Доказать, что Р – искомая точка 2.Вывод.
пересечения прямой и плоскости.
№ 42. Треугольник APD и трапеция ABCD имеют общую сторону AD и лежат в разных плоскостях. Через основание ВС трапеции и середину отрезка PD – точку К проведена плоскость, которая пересекает прямую АР в точке М. Найти МК, если AD = 10.
План решения.
1. l – линия пересечения плоскостей
2. M – точка пересечения прямой АР
и плоскости ВСК.
3. МК – средняя линия DAPD, MK=5.
№ 43 (устно).Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны. Доказать по рисунку 74.
№ 44. В правильной треугольной пирамиде SABC сторона основания а и боковое ребро в. Провести в этой пирамиде плоскость через середины рёбер АВ и ВС параллельно ребру SB. Определить периметр полученного сечения.
План построения.
2. MPÌSAB, MP || SB.
3. NQÌBSC, NQ || SB.
5. MNQР – сечение.
6. Обосновать построение сечения.
1. MN. 2. MP. 3. PMNQP.
Ответ:
№ 45. Построить сечение правильной четырёхугольной пирамиды, проходящее через середины двух смежных сторон основания и середину высоты. Вычислить периметр полученного сечения, если каждое ребро пирамиды равно а.
План построения.
Пусть точки K, F – середины смежных сторон АВ и ВС основания пирамиды,
Р — середина высоты .
2. В плоскости ASC через точку Р
построить MN || AC (рис. 76).
4. QP. 5. L = QP Ç SD (рис. 77).
6. Обосновать, что KMLNF–
искомое сечение (рис. 78).
1. KF. 2. MK. 3. LQ. 4. LP. 5. Вид D MLN. 6. Вид D LPN. 7. PN. 8. LN. 9. PKMLNF.
Ответ:
№46(устно). Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через вершины А, С и точку М ребра A1B1.
2. АМРС – искомое сечение.
3.Обосновать, что АМРС–
искомое сечение (рис. 79).
№ 47 (устно). Через вершину тетраэдра проведена плоскость, параллельная противолежащей грани. Как построить линии пересечения этой плоскости с плоскостями остальных граней тетраэдра?
Назвать линии пересечения плоскости α с гранями BPA, APC, BPC и обосновать выбор.
№ 48. В кубе ABCDA1B1C1D1 середины К и L противолежащих рёбер АА1 и СС1 соединены отрезками прямых с вершинами куба В и D1. Определить вид получившегося четырёхугольника KBLD1 и найти его стороны и диагонали. Ребро куба равно а.
ромб;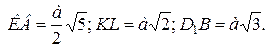
№ 49. В правильной четырехугольной призме ABCDA1B1C1D1 AB=1, AA1=4. Построить сечение призмы, параллельное АС и проходящее через точки D1 и К – середину AA1. Вычислить площадь полученного сечения.
План построения.
6. Обосновать, что D1KBК1 – искомое
2. КК1. 3. D1В.4. S .
№ 50. Основанием правильной призмы служит шестиугольник со стороной 3 дм; высота призмы равна 13 дм. Определить площадь сечения, проведённого через две противолежащие стороны верхнего и нижнего оснований призмы.
1. Х – точка пересечения прямой FE и плоскости грани СС1DD1.
6. Обосновать, что FMB1C1NE – искомое сечение.
1. =2SFMNE.
2. MN. 3. NE. 4. PN. 5. PE. 6. SFMNE.
7. Ответ: 63 дм 2 .
№ 51. На параллельных плоскостях α и β выбрано по паре точек А1, А2 и В1, В2 соответственно так, что прямые А1В1 и А2В2 пересекаются в точке S. Вычислить SA1 и SB2, если А1В1=6 см, SA2=2,5 см SB2 : SA2=3.
План решения.
2. Коэффициент подобия.
Ответ: 1,5 см; 7,5 см.
Рассмотреть иное расположение заданных геометрических фигур (рис. 86) и решить задачу для второго случая.
Ответ: 3 см и 7,5 см.
№ 52. Три прямые, проходящие через одну точку и не лежащие в одной плоскости, пересекают одну из параллельных плоскостей в точках А1, В1 и С1, а другую – в точках А2, В2 и С2. Докажите, что треугольники А1В1С1 и А2В2С2 подобны.
Указание.
Доказать пропорциональность сторон
Рассмотреть иное расположение заданных геометрических фигур и решить задачу для второго случая.
№ 53. В правильной треугольной пирамиде SABC через SD и СЕ, где D – середина АВ, Е – середина SA проведены сечения пирамиды, параллельные между собой. Определить площадь большего из них, если площадь меньшего равна Q.
1. ÐSDР = ÐEMС = j. 2. Выразить площадь D SDР через SD, DР и j.
3. Выразить SD через ME. 4. Выразить DР через MC.
5. Выразить площадь D SDР через ME, MC и j .
6. Выразить площадь D SDР через площадь D MEC. Ответ: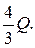
Последнее изменение этой страницы: 2016-04-19; Нарушение авторского права страницы
